Τι είναι τα μοντέλα στο Data Science

• Σχετικά με
• τελευταίες δημοσιεύσεις

Stratos Matzouranis

Το ταξίδι άρχισε το 2008 όπου ξεκίνησα να εργάζομαι επίσημα στον τομέα της τεχνολογίας πληροφορικής (IT). Ξεκινώντας το πρώτο εξάμηνο της σχολής κατάλαβα μια ιδιαίτερη έλξη προς τις βάσεις δεδομένων και τους αυτοματισμούς.Έχω ασχοληθεί με βάσεις δεδομένων όπως Microsoft SQL Server / Oracle Database, ανάλυση δεδομένων και αυτοματισμούς με τη χρήση γραμμής εντολών (CLI), Visual Basic for Applications και Python. Μέσα από τα χρόνια εμπειρίας εξέλιξα αυτές τις δυνατότητες ώστε να μπορώ να κάνω τη ζωή μου πιο εύκολη. Για μένα ο σκοπός του κάθε IT guy αλλά και κάθε υπαλλήλου γραφείου είναι το να έχει τις γνώσεις ώστε μέσω εργαλείων να μπορεί να δουλεύει λίγο αλλά να παράγει πολύ. Μέσα από αυτό τον ιστότοπο του DataPlatform.gr προσπαθώ να προσφέρω γνώσεις και να προτείνω λύσεις σε καθημερινά προβλήματα.

Πιστοποιήσεις:

Τελευταίες δημοσιεύσεις από Stratos Matzouranis (Προβολή όλων)

• Πώς αυτοματοποιούμε τη διαδικασία ελέγχου ακεραιότητας των βάσεων δεδομένων σε SQL Server χωρίς την χρήση maintenance plan - 10 Μάιος 2024
• Πώς μπορούμε να συνδέσουμε Oracle Database με SQL Server με χρήση Oracle Gateway σε Windows - 5 Απρίλιος 2024
• Πώς μπορούμε να λαμβάνουμε email κάθε φορά που ξεπερνάει ένα όριο η μνήμη PGA σε βάση δεδομένων της Oracle - 1 Μάρτιος 2024

Τι είναι τα models στο Data Science;

Με μία απλή πρόταση είναι μοντέλα φτιάχνονται ώστε να μπορούμε να κάνουμε προβλέψεις για μια τάση που ερευνούμε.

Υπάρχουν δύο κατηγορίες μοντέλων τα supervised που τα εκπαιδεύουμε εμείς και στα unsupervised που γίνεται μέσω neural networks.

Στο άρθρο θα ασχοληθούμε με την πρώτη κατηγορία που έχει 3 υποκατηγορίες regression, classification και decision tree.

Οι πιο γνωστές κατηγορίες όταν χρησιμοποιούμε regression

Η Linear που προσπαθούμε με μία ευθεία γραμμή να περάσουμε από όλα τα σημεία των τιμών.

Η Polynomial που αναλόγως τον βαθμό της μπορούμε να χρησιμοποιήσουμε πολλαπλές παραμέτρους ώστε να πλησιάζει περισσότερα σημεία.

Το πρόβλημα που δημιουργείται

Πολλές φορές είναι η σωστή ισορροπία καθότι όσο πιο πολύ ταιριάζει το μοντέλο στα σημεία υπάρχει μεγαλύτερη πιθανότητα μελλοντικά σημεία να έχουν μεγαλύτερη απόκλιση και έτσι έχουμε overfitting.

Underfitting έχουμε όταν το μοντέλο δεν περνάει από τα περισσότερα σημεία τότε ίσως θα πρέπει να αλλάξουμε είδος μοντέλου ή να αυξήσουμε τα degrees/folds.

To κάθε μοντέλο χρειάζεται να γίνει train στην αρχή με ένα ποσοστό δεδομένων και το υπόλοιπο ποσοστό χρησιμοποιείται για test.

Το πόσο ακριβές είναι το μοντέλο

Διακρίνεται με τις τιμές του R^2 (πόσο μικρή απόκλιση έχουν οι τιμές από την γραμμή του μοντέλου) με τιμές από 0~1.

Όπως επίσης από το RMSE (το τετράγωνο του μέσου όρου της διαφοράς το προβλεπόμενων τιμών από τις πραγματικές) με τιμές πάνω από το μηδέν και όταν λέμε μηδέν σημαίνει ότι έχουμε το τέλειο μοντέλο που το θέτει ως αδύνατο.

Αναλυτικό παράδειγμα

Για αρχή θα φορτώσουμε όλες τις βιβλιοθήκες που ίσως χρειαστώ ώστε να μην μπλέξουμε μετά.

import itertools

import numpy as np

import matplotlib.pyplot as plt

from matplotlib.ticker import NullFormatter

import pandas as pd

import numpy as np

import matplotlib.ticker as ticker

from sklearn import preprocessing

from sklearn.ensemble import RandomForestRegressor

from sklearn.linear_model import RidgeClassifier

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier

from sklearn.metrics import f1_score

from sklearn.metrics import jaccard_similarity_score

from sklearn import svm

from sklearn import preprocessing

from sklearn.impute import SimpleImputer

from sklearn.linear_model import Ridge

from sklearn.linear_model import LinearRegression

from sklearn.preprocessing import StandardScaler,PolynomialFeatures

import seaborn as sns

%matplotlib inline

#!conda install -c anaconda seaborn -y

Φορτώνουμε σε ένα dataframe ένα csv με στοιχειά αυτοκινήτων, κρατάμε όσες στείλες θέλουμε και κάνουμε και μία τροποποίηση ώστε να έχουμε τη μέση κατανάλωση.

df = pd.read_csv('https://gist.githubusercontent.com/smatzouranis/acd3354f30ecc1e7cb90caee84650c3a/raw/61adad1fca973303f4af8bc378b3a5432b7371e7/autos_csv.csv')

df = df[['make','fuel-type','horsepower','city-mpg','highway-mpg','price']]

df['AVG-mpg'] = (df['city-mpg']+df['highway-mpg'])/2

dff = df[['make','fuel-type','horsepower','AVG-mpg','price']]

dff.head()

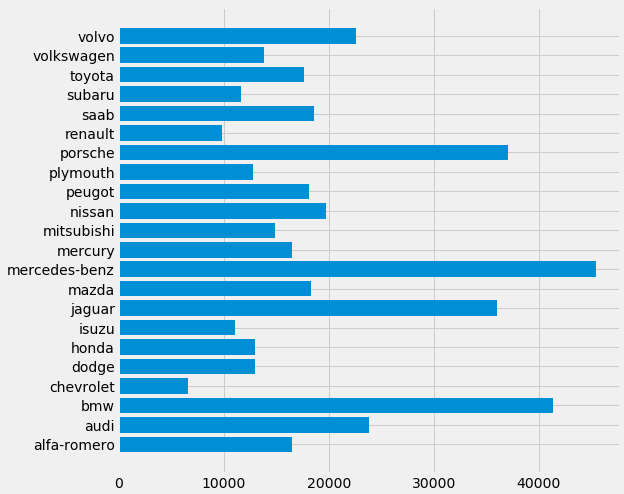
Bar plot

Ας φτιάξουμε ένα γρήγορο bar plot με το κόστος άνα μάρκα.

Θέλει μόνο 5 γραμμές εντολών.

makers = dff['make']

prices = dff['price']

fig, ax = plt.subplots(figsize=(8, 8))

plt.style.use('fivethirtyeight')

ax.barh(makers, prices)

Προετοιμασία των δεδομένων

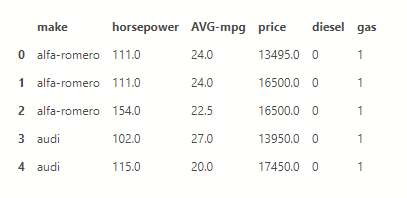
Επειδή είχαμε κείμενο στο τι καύσιμο έχει το κάθε όνομα θα φτιάξουμε καινούργιες στήλες μία για πετρέλαιο και μία για βενζίνη με 0 ή 1 ανάλογα το τι έχει με την εντολή .get_dummies και για να περάσει η αλλαγή χρειάζεται την παράμετρο inplace=True

dff = pd.concat([dff,pd.get_dummies(dff['fuel-type'])], axis=1)

dff.drop(['fuel-type'], axis = 1,inplace=True)

dff.head()

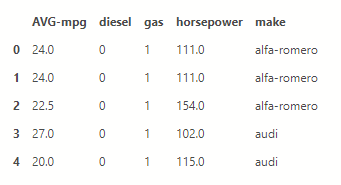
Τώρα θα γεμίσουμε σε όσα αυτοκίνητα δεν έχουν τιμή μια μέση τιμή από τα υπόλοιπα.

X = dff[dff.columns.difference(['price'])]

X =X.fillna(X.mean())

X.head()

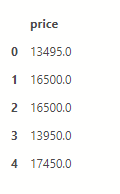
y = dff[['price']]

y =y.fillna(y.mean())

y[0:5]

Linear regression

Μέσα από την βιβλιοθήκη seaborn κάνουμε ένα γρήγορο linear regression plot ώστε να δούμε πως αυξάνεται το κόστος ως προς την ιπποδύναμη με μόνο μία γραμμή κώδικα.

ax = sns.regplot(x='horsepower', y='price', data=dff)

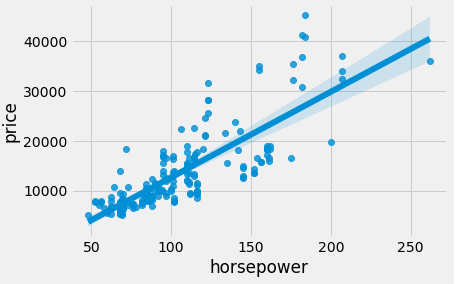
Φτιάχνουμε 2 functions ώστε μπορούμε γρήγορα και εύκολα να φτιάξουμε τα γραφήματα.

def DistributionPlot(RedFunction,BlueFunction,RedName,BlueName,Title ):

    width = 12

    height = 10

    plt.figure(figsize=(width, height))

    ax1 = sns.distplot(RedFunction, hist=False, color=”r”, label=RedName)

    ax2 = sns.distplot(BlueFunction, hist=False, color=”b”, label=BlueName, ax=ax1)

    plt.title(Title)

    plt.xlabel('Τιμή σε δολλάρια')

    plt.ylabel('Χαρακτηριστικά')

    plt.show()

    plt.close()

def PollyPlot(xtrain,xtest,y_train,y_test,lr,poly_transform):

    width = 12

    height = 10

    plt.figure(figsize=(width, height))

    xmax=max([xtrain.values.max(),xtest.values.max()])

    xmin=min([xtrain.values.min(),xtest.values.min()])

    x=np.arange(xmin,xmax,0.1)

    plt.plot(xtrain,y_train,'ro',label='Training δεδομένα')

    plt.plot(xtest,y_test,'go',label='Test δεδομένα')

    plt.plot(x,lr.predict(poly_transform.fit_transform(x.reshape(-1,1))),label='Προβλεπόμενα')

    plt.ylim([-10000,60000])

    plt.ylabel('Price')

    plt.legend()

Χωρισμός δεδομένων σε Train και Test

Χωρίζουμε τα δεδομένα σε training και test με ποσοστό 70-30.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

print("number of test samples :", X_test.shape[0])

print("number of training samples:",X_train.shape[0])

number of test samples : 62

number of training samples: 143

Βαθμολόγηση του μοντέλου

Ορίζουμε σε μια μεταβλητή την κλάση που θα χρησιμοποιήσουμε και ξεκινάμε το training με τα δεδομένα. Έπειτα με το score βλέπουμε ότι το R^2 είναι 0.33 που δείχνει ότι η γραμμή δεν περνάει από τα περισσότερα σημεία.

lre = LinearRegression()

lre.fit(X_train[['horsepower']],y_train)

lre.score(X_test[['horsepower']],y_test)

0.3331272902078515

Cross-validate

Μπορούμε να κάνουμε cross validate to score με τον κάτωθι τρόπο χωρίζοντας τα δεδομένα σε 4 κομμάτια και τεστάροντας το καθένα ξεχωριστά.

Rcross=cross_val_score(lre,X[['horsepower']], y,cv=4)

print("The mean of the folds are", Rcross.mean(),"and the standard deviation is" ,Rcross.std())

The mean of the folds are 0.4392710840512933 and the standard deviation is 0.16681254993011282

Η πρόβλεψη της τιμής

Πάμε να δοκιμάσουμε να φτιάξουμε ένα μοντέλο που να προβλέπει την τιμή από τα χαρακτηριστικά  του  αυτοκινήτου.

lre = LinearRegression()

lre.fit(X_train[['horsepower', 'AVG-mpg', 'diesel', 'gas']],y_train)

lre.score(X_test[['horsepower', 'AVG-mpg', 'diesel', 'gas']],y_test)

0.40859095219326313

Ορίζουμε τις προβλεπόμενες τιμές ως yhat. 

yhat_train=lre.predict(X_train[['horsepower', 'AVG-mpg', 'diesel', 'gas']])

yhat_train[3:7]

array([[21400.06711013],
       [ 9861.84714747],
       [ 4442.33687254],
       [ 5784.42153314]])

Βλέπουμε ότι δεν είχαμε καλή  ακρίβεια στο μοντέλο μας

Η ακρίβεια του μοντέλου

Title='Train Data – Γράφημα προβλεπόμενων data vs actual data'

DistributionPlot(y_train,yhat_train,"Πραγματικά","Προβλεπόμενα",Title)

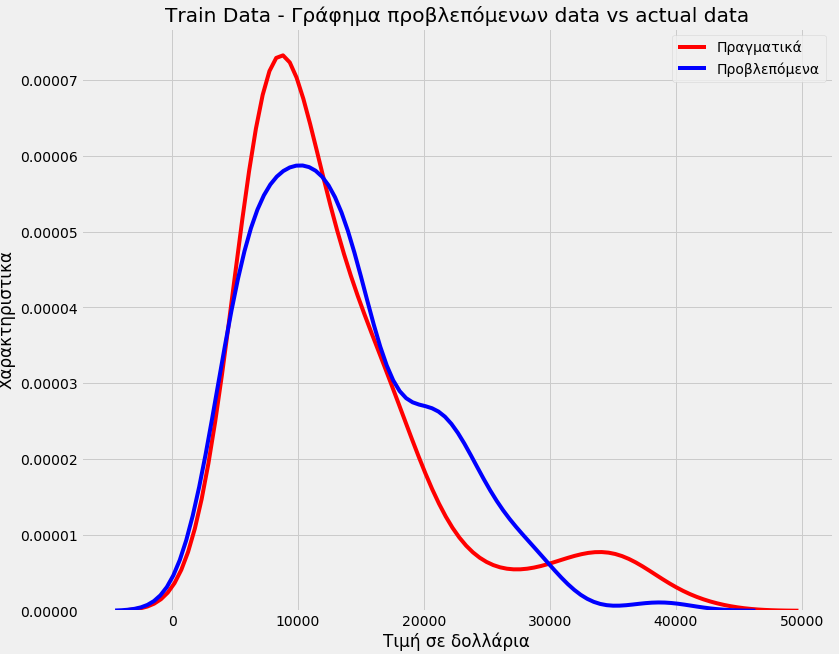
Title='Test Data – Γράφημα προβλεπόμενων data vs actual data'

DistributionPlot(y_test,yhat_test,"Πραγματικά","Προβλεπόμενα",Title)

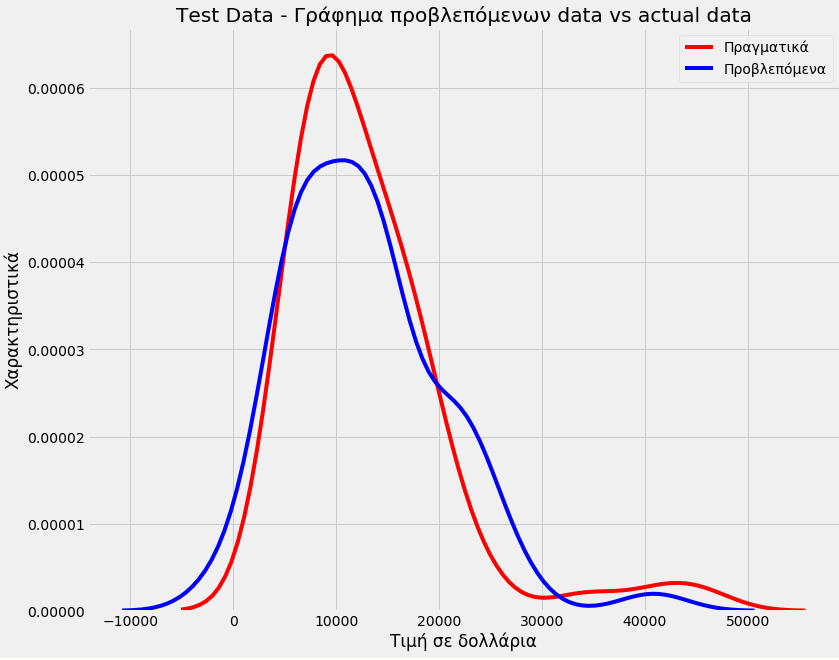
Polynomial αλλά τι βαθμού;

Πάμε σε polynomial 5 βαθμού να δούμε αν θα  έχουμε κάτι καλύτερο. Αυτή την φορά μόνο με τους ίππους.

pr=PolynomialFeatures(degree=5)

X_train_pr=pr.fit_transform(X_train[['horsepower']])

X_test_pr=pr.fit_transform(X_test[['horsepower']])

poly = LinearRegression()

poly.fit(X_train_pr, y_train)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

yhat=poly.predict(X_test_pr)

print("Προβλεπόμενες τιμές:", yhat_test[0:4])

print("Πραγματικές τιμές:",y_test[0:4].values)

Προβλεπόμενες τιμές: [[ 5524.18191454]
 [21532.75818567]
 [14610.3150921 ]
 [ -995.04541995]]
Πραγματικές τιμές: [[ 6795.]
 [15750.]
 [15250.]
 [ 5151.]]

PollyPlot(X_train[['horsepower']],X_test[['horsepower']],y_train,y_test,poly,pr)

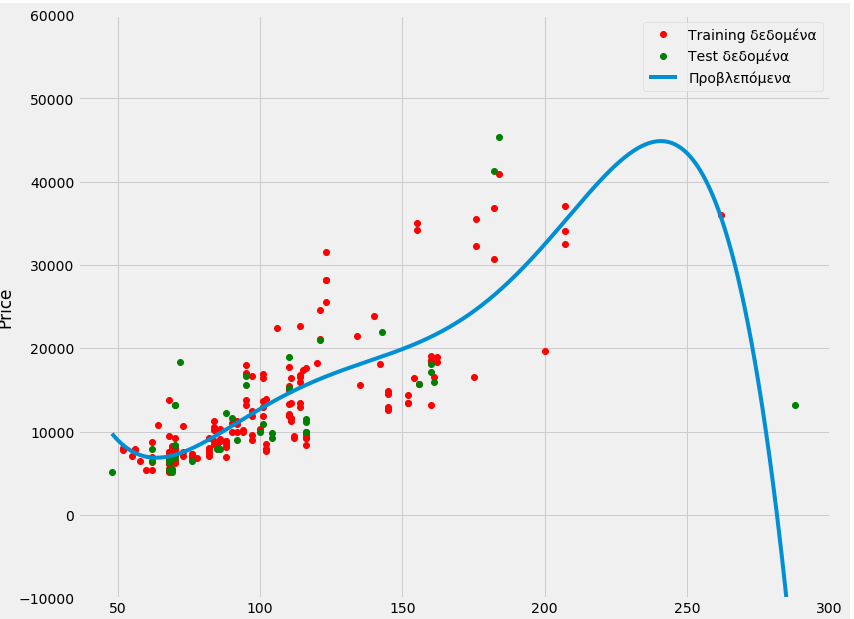
Βλέπουμε μια βελτίωση.

poly.score(X_train_pr,y_train)

0.6830658437904327

poly.score(X_test_pr,y_test)

0.6830658437904327

Μπορούμε να φτιάξουμε ένα loop που δοκιμάζει την διαδικασία με διαφορετικούς βαθμούς ώστε να επιλέξουμε το καλύτερο.

Rsqu_test=[]

order=[1,2,3,4]

for n in order:

    pr=PolynomialFeatures(degree=n)

    X_train_pr=pr.fit_transform(X_train[['horsepower']])

    X_test_pr=pr.fit_transform(X_test[['horsepower']])    

    lre.fit(X_train_pr,y_train)

    Rsqu_test.append(lre.score(X_test_pr,y_test))

plt.plot(order,Rsqu_test)

plt.xlabel('order')

plt.ylabel('R^2')

plt.title('R^2 με χρήση Test Data')

plt.text(3, 0.75, 'Maximum R^2 ') 

Text(3, 0.75, 'Maximum R^2 ')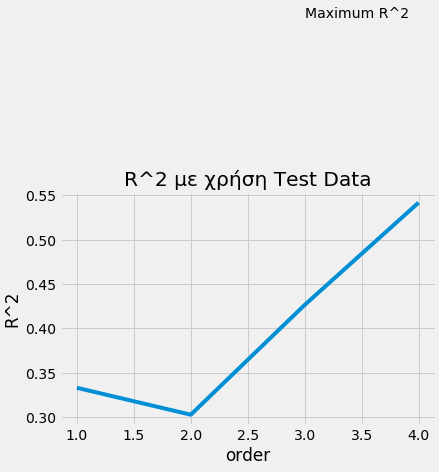

Ridge model

Κάνουμε και μια τελευταία δοκιμή με το rigde model να δούμε αν θα έχουμε ακόμα καλύτερη ακρίβεια.

pr=PolynomialFeatures(degree=2)

X_train_pr=pr.fit_transform(X_train[['horsepower', 'AVG-mpg', 'diesel', 'gas']])

X_test_pr=pr.fit_transform(X_test[['horsepower', 'AVG-mpg', 'diesel', 'gas']])

RigeModel=Ridge(alpha=0.01)

RigeModel.fit(X_train_pr, y_train)

yhat=RigeModel.predict(X_test_pr)

print('predicted:', yhat[0:4])

print('test set :', y_test[0:4].values)

predicted: [[ 6807.95323245]
 [20468.43090602]
 [14849.82259996]
 [10178.31016628]]
test set : [[ 6795.]
 [15750.]
 [15250.]
 [ 5151.]]

Rsqu_test=[]

Rsqu_train=[]

dummy1=[]

ALFA=5000*np.array(range(0,2))

for alfa in ALFA:

    RigeModel=Ridge(alpha=alfa) 

    RigeModel.fit(X_train_pr,y_train)

    Rsqu_test.append(RigeModel.score(X_test_pr,y_test))

    Rsqu_train.append(RigeModel.score(X_train_pr,y_train))

width = 12

height = 10

plt.figure(figsize=(width, height))

plt.plot(ALFA,Rsqu_test,label='validation data  ')

plt.plot(ALFA,Rsqu_train,'r',label='training Data ')

plt.xlabel('alpha')

plt.ylabel('R^2')

plt.legend()

<matplotlib.legend.Legend at 0x7f32d8769358>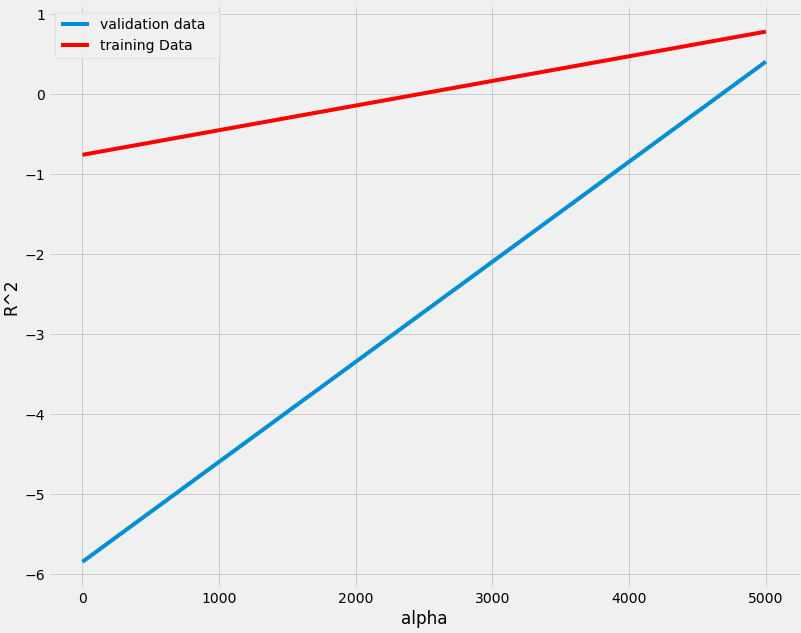

Έπειτα από ένα TLDR post νομίζω θα πήρατε μία ιδέα.

Σίγουρα θα σας φαίνονται δύσκολα και πολύπλοκα αλλά με την χρήση και την εμπειρία λόγο του ότι ο κώδικας που απαιτείται είναι λίγων γραμμών η καθημερινή χρήση τους θα γίνει είναι εύκολη.